
La diffusione di Homo sapiens su tutta la Terra ha avuto e ha tuttora una conseguenza drammatica: la diminuzione della biodiversità, sia locale sia globale. Già nel 1993 il biologo statunitense Edward O. Wilson stimò una perdita di 30.000 specie all’anno: è un calcolo incerto, basato su una valutazione ipotetica del numero totale, poiché la maggior parte delle specie viventi è ancora sconosciuta.
Da quando Homo sapiens ha iniziato a colonizzare la Terra, uscendo dal continente africano, il tasso di estinzione è aumentato senza sosta: la nostra specie rappresenterebbe perciò la peggiore catastrofe biologica da 65 milioni di anni a questa parte, cioè dall’estinzione che portò con sé anche i dinosauri (la quinta, secondo il conto delle grandi estinzioni).
È in corso la «sesta estinzione» in massa dei viventi. Le sue cause sono state riassunte con l’acronimo inglese HIPPO: Habitat destruction (distruzione degli habitat), Invasive species (specie invasive), Pollution (inquinamento), human over-Population (sovrappopolamento umano), Overharvesting by hunting and fishing (sovrasfruttamento mediante caccia e pesca). Anche il cambiamento climatico d’origine antropica è una conseguenza diretta di queste cause. Ma siamo sicuri di essere realmente dispiaciuti? La biodiversità piace agli esseri umani?
Se pensiamo a ciò che realmente soddisfa i nostri gusti, non pare sia sempre così. Anzi. Se escludiamo i naturalisti e pochi altri appassionati di natura, la maggior parte delle persone preferisce un prato all’inglese, formato da una sola pianta erbacea, a un campo invaso da erbacce, un termine dispregiativo usato per definire la moltitudine di specie erbacee che colonizzano gli ambienti incolti.
Carducci avrebbe composto un inno alla biodiversità e al suo magnifico disordine, se, invece dei cipressi che a Bolgheri alti e schietti van da San Guido in duplice filar, il viale fosse stato affiancato da alberi e arbusti delle più svariate forme e specie cresciuti spontaneamente e privi di alcun ordine? Probabilmente no. Anche sui balconi e nei giardini privati si preferisce avere vasi con una sola pianta che emerge dalla nuda terra priva di altri vegetali.
Una delle principali attività dei giardinieri è l’eliminazione di piante estranee alle coltivazioni che accrescerebbero la biodiversità di parchi e aiuole. Persino le foreste si vorrebbe fossero private degli arbusti che formano il sottobosco, per lasciar posto soltanto ad alberi coetanei della medesima altezza. La visione di boschi che ospitano alberi di svariate dimensioni e specie, con un ricco sottobosco occupato anche da piante morte, crollate a terra e consumate da funghi, larve di insetti e molto altro, dà un’idea di incuria, come se la naturale diversità fosse un inutile fastidio. Razionalmente auspichiamo la difesa della biodiversità, mentre inconsciamente vorremmo essere gli architetti dell’ambiente naturale/artificiale. Perché accade ciò nel nostro cervello?
Misurare la biodiversità
La percezione di «disordine» che ci trasmettono gli ambienti naturali ricchi di biodiversità e che ci induce a usare il dispregiativo «erbacce» non è solo una sensazione. Questo disordine, tipico della biodiversità, è vero: lo si può misurare come ogni grandezza fisica misurabile, e misurare la biodiversità non è utile solo per soddisfare la nostra curiosità. Misure oggettive della biodiversità sono necessarie per valutare lo stato di salute sia di un ecosistema, sia della biosfera nel suo complesso, anche al fine di porre rimedio al deterioramento di una situazione ambientale, prima che sia troppo tardi. Misure della biodiversità servono anche per valutare l’importanza ecologica di un ambiente naturale, in modo da decidere quali tutele mettere in atto, come accade per le zone da destinare a riserva naturale. Quantificare la biodiversità non è però facile, anche perché esistono vari livelli di biodiversità – genetica, di specie e di ecosistemi –, e ogni misura si riferisce a uno specifico livello. È alla biodiversità di specie che ci riferiamo abitualmente, ed è questa che cercheremo di definire di seguito.
La biodiversità di specie non si misura semplicemente contando quante specie sono presenti in un habitat (ricchezza in specie). Spesso è necessario confrontare questo numero con altri parametri, come la frequenza relativa. Infatti, se in due ambienti diversi è presente lo stesso numero di specie, ma ciascuna con un’abbondanza differente, la biodiversità cambia. Potrebbe essere il caso di due ipotetici boschi di cento alberi, appartenenti a sole quattro specie: il primo formato da 25 esemplari per ciascuna specie, il secondo da 97 esemplari di una specie e 1 per ciascuna delle altre tre. La biodiversità, se misurata correttamente, deve avere valore minore per il secondo bosco, perché una specie è dominante e le altre tre potrebbero essere sull’orlo dell’estinzione.
Il matematico statunitense Claude Shannon (1916-2001), il padre della teoria dell’informazione, formulò un indice che permette di misurare la biodiversità di specie considerando non solo il numero di specie, ma anche l’uniformità della loro distribuzione. Shannon fu il grande teorico dell’informazione e contribuì a dare un senso ai famosi gigabyte (i famosi giga di cui si parla spesso a proposito del credito telefonico!). L’idea nasce dall’evidenza che, per descrivere un ambiente vario e ricco di biodiversità, sono necessarie più informazioni di quelle che servono per descriverne uno uniforme e monotono. Perciò si usa una formula per calcolare precisamente queste informazioni e definirle con un’unità di misura oggettiva. La domanda cui questa formula risponde è: quante informazioni sono necessarie per descrivere un determinato dato? La formula definisce il contributo di ciascun elemento al contenuto informativo (I) di un insieme di elementi scelti tra diverse possibilità ed è la seguente:
I = – log2p
dove p è la probabilità che capiti ciascun dato elemento e I (il contenuto informativo) è misurato in bit.
Ed è proprio il bit (binary information unit) l’unità di misura dell’informazione; è un sottomultiplo del più comune Byte (otto bit corrispondono a un byte). Maggiore è il numero di bit ottenuto da questo calcolo delle probabilità, maggiori sono le informazioni necessarie per descrivere un dato o una situazione. Alla fine di questo articolo sono riportati esempi di conti che quantificano informazioni e biodiversità. Non sono procedimenti particolarmente complessi, ma è possibile seguire la trattazione anche senza leggerli.
Ordine e disordine, serenità e disagio
Dai calcoli eseguiti con il metodo di Shannon si ottengono alla fine dati precisi e interessanti. La biodiversità arborea del filare di cipressi di Bolgheri sarà pari a zero bit, quella di un bosco con una specie di alberi, accompagnata da rari esemplari di altre tre specie, sarà 0,24 bit, mentre un bosco con quattro specie di alberi tutte ugualmente frequenti è ben 2 bit (pensando ai filari di Bolgheri, dovremmo dedurre che, almeno per Carducci, il tasso di poeticità è inversamente proporzionale al numero di bit…).
Il calcolo della biodiversità di specie, secondo Shannon, è analogo a quello che si esegue per valutare l’entropia: una grandezza che è tanto maggiore quanto più elevato è il grado di «disordine» di un sistema. In effetti, se un bosco fosse parte di un ipotetico ecosistema costituito da una sola specie arborea, magari con alberi coetanei ben allineati, il disordine sarebbe minimo. Un prato all’inglese formato da una sola pianta erbacea ha una biodiversità valutabile in zero bit, minima rispetto a un campo abbandonato invaso da erbe di moltissime specie. Ecco perché la sensazione di “disordine” che si percepisce negli ambienti naturali ricchi di biodiversità non è solo un’impressione: il disordine è reale. Viali alberati monospecifici, fioriere con un solo tipo di fiore e parchi urbani perfettamente ordinati forniscono sensazioni rassicuranti al cervello umano, che potrebbe essere maggiormente a disagio o comunque fare più fatica in situazioni non rappresentabili con semplici schemi mentali, anche se i «caotici» ambienti naturali sono ecologicamente più ricchi.
E così, mentre la parola biodiversità piace molto e la sua difesa è un obiettivo condiviso da tanti, la tentazione di strappare le erbacce per avere il vaso sul balcone con una sola pianta di geranio è irrefrenabile. Magari saremo attivisti di associazioni ambientaliste e non siamo poeti, ma probabilmente preferiamo comunque un giardino a zero bit! Più verosimilmente, la nostra mente è costretta a fare un lavoro in più nei «caotici» ambienti naturali.
Ma forse c’è anche un altro fattore da prendere in considerazione. Homo sapiens ha passato gran parte della sua storia nelle savane africane, ambienti di praterie infinite con pochi alberi isolati: non sarà proprio ciò che vorremmo ricreare in ogni parco urbano anche in climi che nulla hanno a che vedere con le savane cui siamo ben adattati? Se fossimo ancora poche centinaia di migliaia di primati africani che si aggirano nelle savane, il mondo sarebbe splendidamente disordinato e non dovrebbe sopportare le manie delle mente umana, uno degli oggetti più complessi e imperfetti dell’universo.
I conti, per chi volesse approfondire…
Infine, propongo un esempio che può aiutare a capire come si quantificano le informazioni. Calcoliamo la quantità di informazioni contenuta nel DNA di una cellula umana, considerando che il DNA è contenuto in strutture, i cromosomi, dotate di circa 6 miliardi di posizioni. Ogni singola posizione di un cromosoma può essere occupata da una base azotata scelta tra quattro possibili (probabilità una su quattro, 1/4) perché il codice genetico utilizza una sorta di alfabeto a quattro lettere, invece che binario come i programmi del computer. Nei nostri cromosomi ci sarà dunque, per ogni singola posizione, un contenuto informativo (I) pari a I = –log21/4 = –log2 2–2 = 2 bit. Dato che l’insieme di tutti i cromosomi di una cellula umana comprende circa 6 x 109 posizioni, il genoma nel suo complesso ha un contenuto informativo di 2 x 6 x 109 bit, vale a dire 12 x 109 bit, cioè 1,5 gigabyte. Per dare un’idea di quante informazioni contiene una singola cellula umana, basti pensare che un DVD a doppio strato contiene un’analoga quantità di informazioni in un supporto del diametro di 12 cm, decine di migliaia di volte lo spazio di circa 1µm (un milionesimo di metro) del nucleo!
Passiamo ora alla biodiversità di specie in un ambiente naturale, limitandoci soltanto alla vegetazione arborea di un bosco, di cui non consideriamo per semplicità piante erbacee, arbustive, animali, funghi e batteri. Se si analizza un ecosistema di questo tipo, la condizione si presenta molto differente da quella del materiale genetico, sia perché le specie di alberi potenzialmente presenti in un punto non sono sempre e solo quattro, sia perché ciascuna specie ha una diversa probabilità di essere presente. Così accade in generale per un insieme di dati a cui si rivolge la teoria dell’informazione; perciò Shannon modificò l’equazione, introducendo la possibilità di avere probabilità differenti per dati diversi; ossia, in questo caso, frequenze diverse per ciascuna specie.
La formula di Shannon per la misura dell’indice di biodiversità di specie (simbolo Hs) è perciò: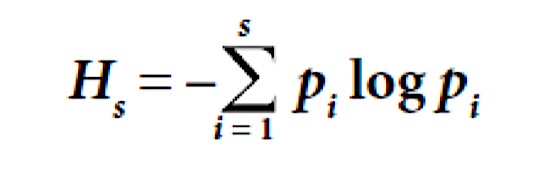
È come scrivere: Hs = – (p1 log p1 + p2 log p2 + … + ps log ps), dove S = numero delle specie e pi = frequenza relativa della i-esima specie, che assume valori tra 0 e 1. Il logaritmo di pi può essere calcolato in base qualunque e ciò determina le unità di misura dell’indice. Si usano comunemente 2, 10 o e (base dei logaritmi naturali); se il logaritmo è in base 2, si ottiene un dato espresso in bit. La sommatoria (∑) permette di tener conto del particolare valore della frequenza relativa per ciascuna specie considerata. Si può provare ad applicare l’equazione per stimare la biodiversità dei due boschi con quattro specie ipotizzate sopra. Nel secondo bosco, quello senza specie dominante, p1 = p2 = p3 = p4 = 0,25; poiché –log2 0,25 = 2, il prodotto pi log pi vale 0,5 in tutti e quattro i casi e la somma dei quattro valori è 2; dunque Hs = 2. Invece, nel primo bosco, quello con una sola specie dominante, p1= 0,97 e p2 = p3 = p4 = 0,01; considerati il calcolo dei logaritmi, i prodotti e la somma finale, si ottiene Hs = 0,24. La biodiversità è circa dieci volte minore, ma piacerà probabilmente di più.

