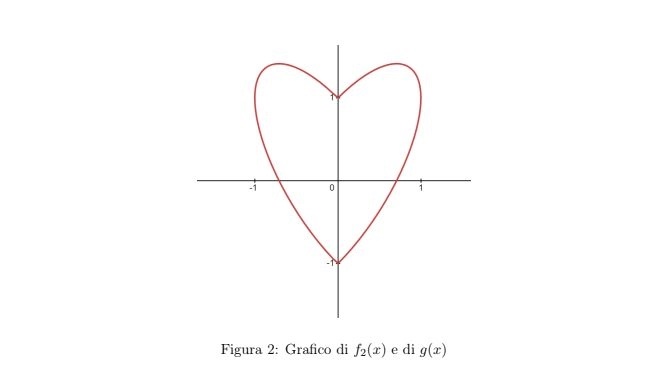
Arrivano a sorpresa nella seconda prova di matematica citazioni, estratti di opere letterarie e situazioni reali. Troviamo infatti ad aprire il secondo problema una frase del matematico italiano Ennio De Giorgi e a chiuderlo un’altra citazione del matematico inglese Godfrey Harold Hardy, che parla della bellezza e dell’armoniosità come requisiti fondamentali non solo per il lavoro di un pittore o di un poeta, ma anche per quello di un matematico. Dopo aver tracciato il grafico richiesto al punto b) del problema, si potrebbe pensare che la scelta della citazione sia stata ispirata dal romantico cuore che si ottiene dall’unione delle due curve.
Interessante è, al quesito 7, la scelta di richiedere di determinare l’equazione di una curva fornendo dati reali: la distanza della Terra dal Sole quando è nei punti di afelio e di perielio. La contestualizzazione degli esercizi di matematica, sempre più richiesta e fondamentale all’interno dei libri di testo, arriva quindi anche all’Esame di Stato, anche se lo fa rischiando di confondere studenti e studentesse con numeri dall’aspetto poco amichevole dati in notazione esponenziale, e soprattutto senza precisare che si sceglie di approssimare con un’ellisse l’orbita terrestre, che un’ellisse in realtà non è.
Oltre alla “matematica e realtà”, caratterizza il quesito 8 anche un tentativo di interdisciplinarità: per presentare il problema è infatti proposto un estratto da L’Adalgisa – Disegni milanesi dello scrittore e ingegnere Carlo Emilio Gadda. Questo esercizio è un esempio di quanto a volte le materie scolastiche siano intrecciate tra loro; e decidere di leggere la lunga (per gli standard di un esercizio di matematica) introduzione è inoltre la parte forse più impegnativa di questo quesito di geometria (nello specifico, di tassellazione del piano), che presenta poi una risoluzione quasi immediata con nozioni apprese già al biennio.
Per quanto riguarda i problemi, rimane una certezza la presenza dello studio di funzione come protagonista. Inaspettato è invece che in entrambi i casi le funzioni siano date con parametri da trovare; si tratta però di un ostacolo facilmente evitabile, dato che, in entrambi i problemi, tre punti su quattro sono risolvibili anche senza dover determinare i temuti parametri.
Il primo problema sembra pensato per chiunque sia arrivato all’esame con le conoscenze previste dalle Indicazioni nazionali: non richiede particolare ragionamento, ma più lunghi ed elaborati sono i calcoli da svolgere per arrivare alle soluzioni.
Il secondo problema parte da una famiglia di funzioni, è meno immediato e richiede quindi maggiore sforzo di ragionamento, ma è caratterizzato da minore quantità e lunghezza di calcoli.
Nella risoluzione del primo problema ci si imbatte però in un dilemma: al punto b) è richiesto di scrivere l’equazione dell’ulteriore retta tangente alla curva passante per il punto . Il punto è però un punto che appartiene alla curva e da esso passa quindi un’unica retta tangente alla curva data. Pensando invece di interpretare la richiesta considerando l’arco di funzione a cui non appartiene (la funzione è discontinua), determinare la retta tangente diventa non banale.
Passando ai quesiti, per chi si è preparato svolgendo le prove degli anni passati, la prima impressione potrebbe essere stata quella di un déjà-vu: dimostrazione da biennio e probabilità nei lanci di un dado truccato come primi due esercizi, proprio come per l’Esame 2023.
Seguono poi quesiti standard di analisi matematica, mentre risultano grandi assenti i limiti e i teoremi fondamentali del calcolo differenziale.