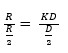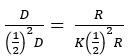Come far appassionare gli studenti delle superiori all’Astronomia? Si tratta di un problema non di semplice soluzione per gli insegnanti di Fisica e di Scienze. Gli approcci possibili sono diversi e dipendono da vari fattori, non per ultimo la disponibilità di strumentazione osservativa, amatoriale o meno che sia. In alcuni casi si può fare qualcosa anche con poco, come ad esempio una semplice macchina fotografica. Quando in classe si affrontano tematiche quali le tecniche per determinare le distanze astronomiche, o quando si parla di dimensione apparente e reale di un oggetto astronomico, o ancora di luminosità apparente ed assoluta, si osserva un certo disorientamento negli alunni dovuto al fatto che spesso non si può specificare nei dettagli le tecniche seguite in astronomia. Come facilmente si può comprendere una descrizione troppo generale non è in grado di coinvolgere più di tanto i ragazzi, anche quelli più motivati. Le attività sperimentali hanno invece il pregio di trascinare gli studenti nel vivo della problematica aprendo le porte per veicolare concetti base delle discipline propedeutiche come la Matematica e la Fisica. In questo breve lavoro si propone una attività sperimentale volta alla determinazione delle distanze alle quali si trovano i pianeti ed il Sole attraverso un metodo basato sull’applicazione di pochi concetti base di Matematica e di Fisica. Con riferimento ai concetti base di tali discipline, necessari e propedeutici alla realizzazione dell’esperienza, l’attività sperimentale proposta si rivolge meglio ad alunni del triennio delle superiori. Inoltre, la ridondante specificazione dei semplici passaggi matematici introdotti si giustifica perché tiene conto della non ancora consolidata formazione scientifica dei lettori a cui ci si rivolge.
Dimensione angolare
In Astronomia il diametro angolare (o dimensione angolare) di un oggetto è la misura del suo diametro rispetto alla distanza dall’osservatore. Esso corrisponde all’angolo che ha per tangente ([1]) il rapporto: DIAMETRO/DISTANZA, ovvero ![]() La formula si basa su uno dei teoremi dei triangoli rettangoli che dice: in un triangolo rettangolo un cateto è uguale al prodotto dell’altro cateto per la tangente dell’angolo opposto al primo. In questo enunciato compare la nozione trigonometrica di tangente di un angolo (PQ nel disegno sotto riportato) intesa come rapporto tra seno e coseno (diametro e distanza nel nostro caso). Si osservi infatti che i due triangoli OPQ e OHM sono in proporzione ovvero:
La formula si basa su uno dei teoremi dei triangoli rettangoli che dice: in un triangolo rettangolo un cateto è uguale al prodotto dell’altro cateto per la tangente dell’angolo opposto al primo. In questo enunciato compare la nozione trigonometrica di tangente di un angolo (PQ nel disegno sotto riportato) intesa come rapporto tra seno e coseno (diametro e distanza nel nostro caso). Si osservi infatti che i due triangoli OPQ e OHM sono in proporzione ovvero:![]()
Inoltre, HM = senγ, OM = cosγ, OQ = raggio circonferenza goniometrica (x2 + y2 = 1) e quindi = 1.
Pertanto, la (1) diventa:
ovvero
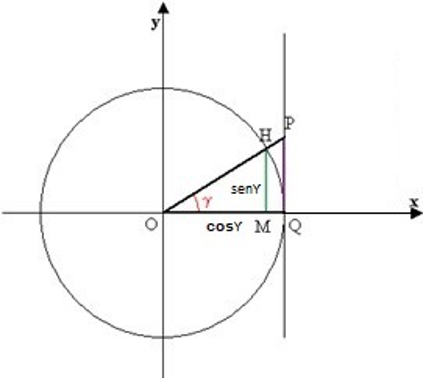
La dimensione angolare di un corpo celeste è possibile conoscerla se si conosce il diametro del corpo e la distanza alla quale esso si trova. Di nuovo ci vengono in aiuto i triangoli rettangoli e la circonferenza goniometrica. Per determinare quindi il diametro di un qualsiasi corpo celeste (senƳ di Fig. 1) una volta conosciuta la distanza (cosƳ di Fig.1) e la dimensione angolare è sufficiente moltiplicare la distanza medesima per la tangente del diametro angolare. Nel caso del Sole (vedi tab. 1) avremo: dimensione angolare media = 1930” = 0,5361111° (1930/3600), distanza =149.600.000 Km. Quindi Diametro = 149.600.000 Km * tan 0,5361111 =1399833,7 Km. Cioè, un raggio di circa 700000 Km, come è noto.
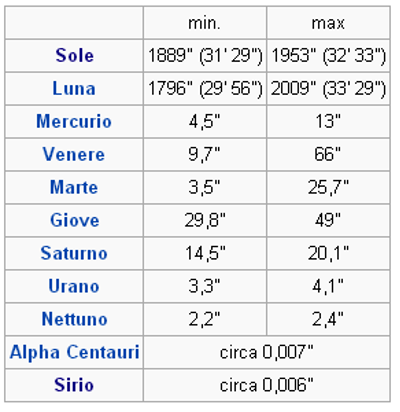
In questo lavoro si vuole descrivere un metodo operativo che permette di risalire al valore della dimensione angolare di un oggetto astronomico ma dopo aver determinato la distanza del corpo celeste attraverso la conoscenza del suo diametro reale e la misura del diametro (o del raggio) della sua immagine impressa su pellicola fotografica. Analogamente, si può raggiungere lo stesso obiettivo determinando il suo diametro reale conoscendo però la sua distanza e misurando il diametro della sua immagine. La tecnica proposta si basa sulla relazione che lega la dimensione apparente di un oggetto alla distanza dall’osservatore alla quale si trova. Di tale relazione si argomenterà nel prossimo paragrafo.
Un approccio diverso per misurare le dimensioni di un oggetto e la sua distanza
È facile verificare, se si osserva un oggetto qualsiasi da due punti diversi posti il secondo a distanza doppia rispetto al primo, che le dimensioni apparenti dell’oggetto osservato si riducono a metà (il suo raggio si dimezza, se l’oggetto ha forma sferica) ovvero che la sua superficie apparente si riduce di quattro volte. Viceversa, se la distanza si dimezza avvicinandoci all’oggetto, la superficie apparente diventa quattro volte maggiore. Se consideriamo un oggetto di forma sferica anche la sezione circolare di quest’ultimo presenterà un raggio che, conseguentemente, si dimezzerà o raddoppierà come infatti ci suggerisce la seguente tabella:
| COLONNA A | COLONNA B | COLONNA C | COLONNA D |
| Raggio (m) | π | Superficie (m2) | Rapporto superficie (valore rigo successivo di colonna C / valore rigo di colonna C) |
| 1 | 3,141… | 3,141… | |
| 2 | 3,141… | 12,566 | 4 |
| 4 | 3,141… | 50,265 | 4 |
| 8 | 3,141… | 201,062 | 4 |
| 16 | 3,141… | 804,248 | 4 |
| 32 | 3,141… | 3217 | 4 |
| 64 | 3,141… | 12868 | 4 |
Fig. 3 – Tabella con parametri relativi al cerchio con raggio che raddoppia reiteratamente.
È possibile verificare sperimentalmente tale relazione in modo molto semplice. Si può ad esempio preparare l’apparato riportato nella foto di Fig. 4.

Si tratta di realizzare due cerchi di cartone di cui uno abbia il raggio doppio dell’altro. Si lega poi ad un treppiedi improvvisato un filo che dall’altro capo viene fissato ad un supporto fisso. Al treppiedi si fissa anche una tavoletta con un foro laterale che serve per potervi guardare attraverso. Come evidenziato nella foto il filo viene fatto passare per il centro geometrico dei due dischi in modo che questi ultimi possano scorrere lungo il filo medesimo e siano in collimazione con il foro praticato sulla tavoletta. Inserendo prima un disco e poi l’altro si può sperimentare che il disco più grande deve essere posto ad una distanza doppia dal foro praticato nella tavoletta, rispetto al disco più piccolo, se si vuole inquadrare pienamente il disco in questione. Solo in tal modo, infatti, i due dischi possono occupare pienamente il cono ottico che si forma traguardando attraverso il foro praticato nella tavoletta, escludendo dalla vista tutto il resto. Evidentemente se il raggio e la superficie del disco rimangono invariate bisogna raddoppiare la distanza alla quale porre il disco per vederlo apparire di diametro dimezzato. Ciò dimostra la relazione sopra ricordata tra dimensione apparente dell’oggetto e distanza dall’osservatore.
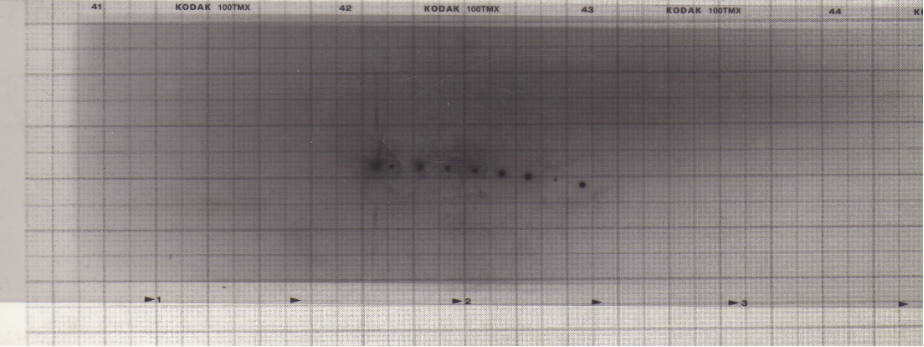
Quindi l’esperienza conferma, dal punto di vista fisico, quanto evidenziato matematicamente con i dati riportati nella tabella di Fig. 3. Infatti, il disco di cartone più grande ha, per costruzione, una superficie quattro volte maggiore del disco più piccolo in quanto il raggio di quest’ultimo è pari a metà di quello del disco più grande. Pertanto, nella realtà se raddoppia la distanza si dimezza il raggio apparente e la superficie diventa quattro volte più piccola. Se si dimezza la distanza raddoppia il raggio apparente e la superficie diventa quattro volte più grande. Si è dunque pensato di applicare tale correlazione per calcolare la distanza di un corpo celeste, quale ad esempio la Luna o un pianeta del sistema solare. A tale scopo si è voluto utilizzare un sistema che prevede, per prima cosa, la misura, come dato di riferimento, del diametro apparente mostrato dal Sole sul negativo di una foto. Tale misura può poi essere posta in correlazione con la dimensione reale del diametro (e quindi del raggio) del Sole stesso. La foto in questione fu scattata qualche tempo fa al nostro Astro con una macchina fotografica con focale 125 mm e con pellicola Kodak 100TMX (vedi foto) ([2]). Per conoscere il valore del diametro apparente del Sole dalla distanza alla quale si trova la Terra è possibile quindi utilizzare il negativo di una foto scattata al nostro Astro in corrispondenza del mezzogiorno locale. Basta infatti sovrapporre al negativo un foglio di acetato trasparente sul quale è stato stampato un reticolo millimetrico. Sottoponendo poi a scansione il negativo con il foglio millimetrato sovrapposto sarà possibile riportare al computer l’immagine ottenuta ed ingrandirla sufficientemente per misurare con una certa precisione il diametro della macchiolina rappresentante il disco solare. Il diametro apparente così misurato è in relazione con quello reale a mezzo della distanza Terra-Sole.
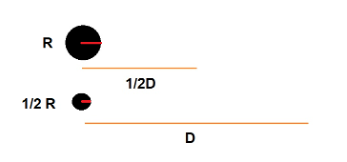
Possiamo anche esprimere matematicamente la relazione di proporzionalità sopra descritta con la seguente uguaglianza, in cui R è il raggio reale dell’oggetto e D la distanza alla quale si trova l’oggetto medesimo, ½ R è il raggio apparente alla distanza D dimezzata:
(2) R : 1/2R = D : 1/2D
Cioè, il rapporto tra raggio maggiore e quello dimezzato deve essere uguale ([3]) al rapporto tra la distanza maggiore e quella dimezzata, a meno di una costante K.
Riscriviamo quindi la (2) tenendo conto della costante K:
Dalla (2a) possiamo dedurre che la superficie apparente finale dell’oggetto possa essere il risultato di un certo numero n di osservazioni reiterate a distanze dalle quali di volta in volta si dimezza il raggio dell’oggetto. La distanza dalla quale si dimezza il raggio dell’oggetto è sempre il doppio della distanza precedente. Quindi, se il dimezzamento del raggio apparente è una conseguenza del raddoppio della distanza, successivi dimezzamenti del raggio saranno il frutto di una serie di raddoppiamenti della distanza, dei quali ogn’uno è pari per dimensioni alla somma dei valori dei vari raddoppiamenti che lo hanno preceduto più il valore della distanza iniziale. Si consideri, a titolo di esempio, la seguente tabella dove vengono riportati dei valori numerici, non riferiti ad oggetti e distanze reali, al fine di esplicitare il concetto.
Quindi possiamo scrivere la (2a) nel seguente modo:
 ([4])
([4])
| COLONNA A | COLONNA B | COLONNA C | COLONNA D | COLONNA E |
| Raggio (m) | π | Superficie (m2) | Rapporto superficie (valore di colonna C/valore successivo di colonna C) | Distanza (m) |
| 64 | 3,141… | 12867,96 | 4 | 100 |
| 32 | 3,141… | 3217 | 4 | 200 |
| 16 | 3,141… | 804,25 | 4 | 400 |
| 8 | 3,141… | 201,06 | 4 | 800 |
| 4 | 3,141… | 50,27 | 4 | 1600 |
| 2 | 3,141… | 12,57 | 4 | 3200 |
| 1 | 3,141… | 3,142 | 6400 |
Fig. 7 – Variazione subita dal raggio del cerchio al raddoppio della distanza
Con n ≥ 1
Posto il primo membro = X ([5]) avremo:
Da cui si ricava:
2n =X
E quindi, sostituendo ad X il suo valore (1,1E12) otteniamo:
n = 40,017
Se adesso andiamo a sostituire al primo membro della (2b) il rapporto tra raggio reale del Sole e quello della sua immagine su pellicola, cioè il valore 1,1E12 ([6]) ed il corrispondente valore a D e ad n nel secondo membro sempre della (2b) ci accorgiamo che il valore di K è uguale a 1. Ciò si verifica perché il valore del denominatore che rappresenta la distanza minima di reiterazione è pari a 134,45 mm [(1/2)40,017 * D = 8,987E-13 * 149600000000000 mm = 134,45 mm]. Ma se imponiamo ([7]) che la distanza minima possa essere la distanza focale della macchina fotografica, che nel nostro caso era 125 mm, possiamo ricavare un differente valore di K. Da un semplice calcolo otteniamo ([8]):
K = 0,93 ([9])
Ci rendiamo quindi conto che, se il rapporto tra raggio solare e raggio dell’immagine solare su pellicola fosse stato leggermente diverso, grazie ad una migliore tecnica fotografica ed una più precisa conseguente misurazione del diametro dell’immagine impressa su pellicola, avremmo ottenuto il valore di 125 mm anziché 134, 45 mm e, come visto sopra, anche in questo caso il valore di K sarebbe stato pari a 1. Per avere una distanza reiterativa minima di 125 mm il raggio medio dell’immagine fotografica del Sole avrebbe dovuto essere pari a 0,581 mm invece di 0,625 mm ([10]). Probabilmente una qualità migliore dell’immagine fotografica confermerebbe un tale valore. Del resto, se prendiamo i due valori della dimensione angolare del Sole riportati nella tabella di Fig. 2 e li trasformiamo in gradi sessagesimali per calcolarne la rispettiva tangente e poi moltiplichiamo il valore di tale tangente per una distanza minima pari alla lunghezza focale della macchina fotografica, otteniamo il diametro dell’immagine fotografica del Sole nei due casi: 1,145 mm e 1,19 mm. Pari ad un raggio di 0,573 mm e 0,595 mm. Il valore ipotizzato di 0,581 mm ricade all’interno dell’intervallo considerato. Quindi per una distanza pari alla distanza focale il calcolo delle dimensioni dell’immagine del Sole, fatto utilizzando la formula della dimensione angolare, conferma le dimensioni apparenti dell’astro misurate sulla pellicola fotografica ([11]).
Adesso sappiamo dalla (2b) che il rapporto tra la distanza reale dell’oggetto e la distanza minima al termine delle reiterazioni è pari al rapporto tra il raggio reale dell’oggetto e quello della sua immagine su pellicola fotografica diviso la costante K:
Considerato che il denominatore del primo membro della (2d) deve essere 125 mm possiamo determinare la distanza D.
Ricordando la (2c) possiamo riscrivere la (2d) nel seguente modo:
(3) D = 125* X/K ([12])
Nel caso che, grazie a misure più precise, venisse confermato sperimentalmente che K = 1 la (3) diventerebbe:
(3a) D = 125* X
L’utilità della (3a) sembra evidente: conoscendo le dimensioni stimate dell’oggetto celeste e misurando le dimensioni della sua immagine fotografica si può risalire alla distanza alla quale si trova.
Vediamo adesso quale potrebbe essere la dimensione dell’immagine fotografica della Luna vista dalla Terra se nella (3) inseriamo i valori della distanza media Terra-Luna e le dimensioni del raggio lunare.
Scriviamo la (3) nel seguente modo:
(3b) D = 125* RL/(Rimm*K)
Dove
RL = raggio lunare (1,7374E+09 mm)
Rimm = raggio dell’immagine fotografica
D = distanza Terra-Luna (3,84E+11 mm)
K = 0,93
Avremo:
Rimm = 0,608
Tale valore è molto vicino a quello del raggio della macchia prodotta sulla nostra pellicola dal Sole (0,625) ([13])! In effetti i due corpi celesti visti dalla Terra presentano, come noto, pressoché la stessa dimensione angolare (vedi tabella 1) perché uno è molto grande ma anche molto lontano e l’altra è molto più piccola ma assai più vicina alla Terra. Quindi la superficie impressa sulla pellicola è in proporzione diretta con le dimensioni del corpo e in proporzione inversa con la distanza del corpo celeste.
Dimensione apparente del sole visto dai pianeti e dimensione apparente dei pianeti visti dalla terra
Proviamo adesso a chiederci con quale dimensione fotografica apparirebbe il Sole in una foto scattata da ciascun pianeta del sistema solare. La seguente tabella, realizzata applicando la (3) ci mostra il risultato del semplice calcolo.
| COLONNA A | COLONNA B | COLONNA C | COLONNA C | COLONNA E |
| Pianeta | D (distanza Pianeta-Sole) mm | Raggio Sole (mm) | K | Raggio immagine (mm) |
| Mercurio | 5,80E+13 | 6,9545E+11 | 0,93 | 1,6E+00 |
| Venere | 1,08E+14 | 6,9545E+11 | 0,93 | 8,6E-01 |
| Terra | 1,496E+14 | 6,9545E+11 | 0,93 | 6,3E-01 |
| Marte | 2,28E+14 | 6,9545E+11 | 0,93 | 4,1E-01 |
| Giove | 7,79E+14 | 6,9545E+11 | 0,93 | 1,2E-01 |
| Saturno | 1,43E+15 | 6,9545E+11 | 0,93 | 6,5E-02 |
| Urano | 2,87E+15 | 6,9545E+11 | 0,93 | 3,3E-02 |
| Nettuno | 4,5E+15 | 6,9545E+11 | 0,93 | 2,1E-02 |
Fig. 8 – Valori del raggio dell’immagine fotografica del Sole visto dalla superficie di ciascun pianeta del sistema solare.
Se invece volessimo sapere quale dimensione fotografica avrebbe ciascun pianeta fotografato dalla terra? Si può fare un calcolo analogo però bisogna tenere in considerazione che la distanza tra il pianeta e la Terra varia continuamente a seconda della sua posizione orbitale come anche di quella della Terra. Ad esempio, la distanza di Giove dalla Terra varia da un minimo di 591000000 Km ad un massimo di 965000000 di Km. Tenendo conto che il raggio del pianeta è di 69911 Km avremo per le due distanze considerate i seguenti valori per quanto riguarda la dimensione dell’immagine su pellicola:
| COLONNA A | COLONNA B | COLONNA C | COLONNA D | COLONNA E |
| Pianeta | D (distanza Giove-Terra) mm | Raggio Giove (mm) | K | Raggio immagine (mm) |
| Giove | 5,91E+14 | 6,99E+10 | 0,93 | 1,6E-02 |
| 9,65E+14 | 6,99E+10 | 0,93 | 9,7E-03 | |
| 7,79E+14 | 6,99E+10 | 0,93 | 1,2E-02 |
Fig. 9 – Valori del raggio dell’immagine fotografica di Giove visto dalla superficie terrestre da varie distanze.
L’ultima riga della tabella di fig.9 riporta la dimensione del raggio dell’immagine prodotta da Giove se consideriamo Giove alla distanza dalla Terra uguale a quella che ha il pianeta dal Sole. Si può notare che il raggio dell’immagine quando si considera Giove posto alla distanza dalla Terra uguale a quella che ha Giove dal Sole risulta essere 9,95 volte più piccola di quella riportata in Fig. 8 (1,201E-1/1,2073E-2 = 9,95). Tale valore è giustificato dal fatto che anche il raggio di Giove risulta essere 9,95 volte più piccolo di quello del Sole (6,9545E+11/6,99E+10 = 9,95).
Analoghi calcoli possono essere facilmente fatti per tutti gli altri pianeti del sistema solare, e non solo. L’utilizzo quindi di buone immagini fotografiche di un corpo celeste permettono, applicando la (3), di calcolare la distanza del corpo dopo averne stimato la dimensione reale. È facile adesso calcolare la dimensione angolare di tutti i corpi del sistema solare visti dalla Terra. È sufficiente applicare la già ricordata formula: ![]() . Se invece si volesse conoscere il diametro del corpo celeste conoscendone la sua distanza e misurandone la dimensione della sua immagine su pellicola si può applicare parimenti la relazione (3b) dalla cui formula inversa si può ricavare il dato cercato.
. Se invece si volesse conoscere il diametro del corpo celeste conoscendone la sua distanza e misurandone la dimensione della sua immagine su pellicola si può applicare parimenti la relazione (3b) dalla cui formula inversa si può ricavare il dato cercato.
Considerazioni conclusive
I dati presentati ci suggeriscono che è possibile dedurre la distanza alla quale si trova un corpo celeste se si possiede una immagine fotografica del corpo medesimo. È dunque possibile proporre a degli studenti del triennio delle superiori una attività sperimentale basata sulla fotografia dei principali corpi celesti del sistema solare e sulla successiva misurazione del diametro apparente mostrato dai corpi medesimi sul relativo fotogramma. Sul principio teorico non influisce l’eventuale utilizzo di sistemi ottici di ingrandimento, certamente consigliabili in diversi casi. Infatti, l’ingrandimento realizzato è sempre noto e quindi la dimensione reale dell’immagine fotografica può sempre essere calcolata. La tecnica presentata in questo breve lavoro è semplice. È sufficiente misurare il raggio dell’immagine del corpo celeste impressa sulla pellicola fotografica e, ipotizzando un raggio reale dell’oggetto astronomico, ricavarne la distanza utilizzando la (3). Ipotizzare il raggio reale non significa proporre un valore a caso ma affidarsi ad altri sistemi di accertamento basati su differenti parametri astronomici come ad esempio la luminosità. Le grandezze fisiche che è necessario conoscere per un compito sono note e si tratta della luminosità apparente, derivante da brillantezza e distanza, e della temperatura superficiale, determinata dal tipo spettrale. A partire da questi dati è possibile applicare poche formule per giungere alla dimensione di una stella ed è proprio in questo modo che gli astronomi hanno proceduto finora per trovare che molte stelle sono più piccole del nostro Sole e molte altre sono più grandi. La legge di Stefan-Boltzmann è utilizzata per determinare la dimensione di una stella. Essa afferma che: l’ammontare di energia che una stella irradia ogni secondo da un metro quadrato della sua superficie è proporzionale alla quarta potenza della sua temperatura superficiale T. In formule, il flusso energetico F di una stella è dato dalla relazione di Stefan-Boltzmann seguente:
(4) F = σT4
La relazione tra flusso F, luminosità L e raggio della stella R è data dalla relazione:
(5) L = 4σR2σT4
dove L è la luminosità della stella espressa in Watt, R è il suo raggio espresso in metri, σ è la costante di Stefan-Boltzmann mentre T è la temperatura superficiale espressa in gradi Kelvin. In tal modo si può ricavare il raggio di un corpo celeste anche piuttosto lontano. Può essere una stella oppure una galassia. Infatti, anche di una galassia si possono stimare le dimensioni attraverso misurazioni della sua massa ([14]). Dedotta la dimensione reale dell’immagine fotografica tenuto conto dell’ingrandimento si può dedurre, di conseguenza, la sua distanza dal Sole.
Oggi tramite ALMA (Atacama Large Millimeter/Submillimeter Array) si è riusciti a ottenere una immagine di Betelgeuse e del suo disco. Analogamente si può fare per altre stelle e/o galassie. Tenendo conto dell’ingrandimento fornito da questa moderna tecnologia osservativa si potrebbe, probabilmente, pensare di ricavare informazioni, mediamente attendibili, sulla distanza alla quale si trovano questi corpi celesti utilizzando le informazioni fornite dai fotogrammi scattati e tramite la semplice tecnica appena descritta.
Sebbene l’utilizzo di macchine fotografiche vecchio tipo, che fanno uso di rullini fotografici, sia diventato ormai obsoleto e i rullini stessi reperibili in commercio con qualche difficoltà, tuttavia, l’attività sperimentale è ancora possibile realizzarla. Certo, la tecnica ipotizzata, anche se affinata da ulteriori misurazioni, mantiene un limite di affidabilità perché la misura delle dimensioni dell’immagine fotografica potrebbe essere poco precisa. Tuttavia, l’utilizzo di migliori apparecchiature ottiche e il ricorso all’analisi computerizzata delle immagini prodotte potrebbe migliorare l’accuratezza del metodo. Per finalità didattiche rimane certamente una interessante esperienza da proporre.
Bibliografia
ASTROLAB: calcolo delle dimensioni angolari. Retrieved from : http://astrolab.altervista.org/articoli/angolo.html
Diametro Angolare – Wikipedia. Retrieved from: https://it.wikipedia.org/wiki/Diametro_angolare
Dimensione e massa in astronomia. Retrieved from: https://www.astronomiamo.it/DivulgazioneAstronomica/Area/Unit%C3%A0%20di%20misura%20in%20Astronomia/Dimensione-e-massa-in-astronomia-tecniche-di-misurazione
- Lupia Palmieri, M. Parotto (2004), Il Globo Terrestre e la sua Evoluzione -quinta edizione. Bologna: Zanichelli
Giove – Wikipedia. Retrieved from: https://it.wikipedia.org/wiki/Giove_(astronomia)
Luna – Wikipedia. Retrieved from; http://it.wikipedia.org/wiki/Luna
Marte – Wikipedia. Retrieved from: https://it.wikipedia.org/wiki/Marte_(astronomia)
Mercurio – Wikipedia. Retrieved from; https://it.wikipedia.org/wiki/Mercurio_(astronomia)
Nettuno – Wikipedia. Retrieved from;: https://it.wikipedia.org/wiki/Nettuno_(astronomia)
Ottica geometrica. Retrieved from: https://www.phys.uniroma1.it/fisica/sites/default/files/file_PLS/OtticaGeometrica.pdf
Saturno – Wikipedia. Retrieved from: https://it.wikipedia.org/wiki/Saturno_(astronomia)
Sole – Wikipedia. Retrieved from: http://it.wikipedia.org/wiki/Sole
Terra – Wikipedia. Retrieved from ; https://it.wikipedia.org/wiki/Terra
Urano – Wikipedia. Retrieved from: https://it.wikipedia.org/wiki/Urano_(astronomia)
Venere – Wikipedia. Retrieved from; https://it.wikipedia.org/wiki/Venere_(astronomia)
NOTE
[1] La tangente è una funzione trigonometrica definita come la proiezione sull’asse del punto di incontro tra il prolungamento del secondo lato dell’angolo orientato e la retta che tange la circonferenza goniometrica nel punto (1,0).
[2] Ingrandendo la foto e misurando con il software grafico Gimp il diametro delle macchie presenti sulla pellicola (escludendo la prima e la terza da sinistra) è stata determinata una media delle misurazioni pari a 1,25 mm, equivalente ad un raggio medio di 0,625 mm. Le immagini prodotte del disco solare sono state ottenute nell’arco di alcune ore a cavallo del mezzogiorno locale. Come è evidente l’immagine realizzata non appare ottimale per una misura precisa della dimensione apparente del Sole. Si tratta di una foto fatta da neofiti della fotografia dove manca una precisa scelta dei tempi di esposizione. Bisognerebbe utilizzare immagini di qualità migliore. Tuttavia, il valore medio calcolato può compensare la variazione dimensionale osservata. Inoltre, la stessa immagine può essere, intanto, utile per illustrare la tecnica seguita. Nell’ipotesi di una reale e riconosciuta validità della tecnica proposta ben più precise e nitide immagini potranno essere utilizzate per l’esecuzione dei calcoli.
[3] In questo caso il rapporto tra primo membro e secondo membro della (2), cioè il valore della costante k, è pari ad 1. Il valore di questo rapporto deve, matematicamente, essere sempre pari a 1. Infatti, entrambi i membri dell’equazione (2) diminuiscono con lo stesso ritmo: dimezza l’uno e dimezza anche l’altro. Pertanto, dopo n dimezzamenti entrambi i due rapporti devono essere uguali. È possibile avere un valore di k diverso da 1 solo se si vuole tenere in considerazioni altri fattori. Ciò è quanto faremo tra breve.
[4] Con i dati della tabella applichiamo la (2b) fino alla quinta reiterazione. Avremo: ![]() e K è pari a 1.
e K è pari a 1.
[5] Il valore di X può essere ricavato dal rapporto tra il raggio reale del corpo e quello della sua immagine su pellicola fotografica. Il rapporto considerato assume il valore di 1,11272E12.
[6] 6,9545E+11/0,625 = 1,11272E12.
[7] Sembra plausibile assumere che la distanza ripetitiva minima possa essere la distanza focale della macchina fotografica perché essa rappresenta la distanza dalla quale è stato fatto l’ultimo rimpicciolimento dell’immagine solare che così è stata ridotta a quella impressa sul fotogramma. In pratica l’obiettivo della macchina fotografica cattura la penultima immagine del Sole che viene rimpicciolita e focalizzata sulla pellicola posta alla distanza di 125 mm. Possiamo quindi immaginare che questa distanza minima raddoppiando ad ogni reiterazione diventi pari alla distanza Terra – Sole dopo n volte. Se vogliamo adesso sapere quanto vale n possiamo porre, il denominatore del secondo membro della (2b) uguale a 125 mm invece che 134,45 mm e ricavare il valore di ![]() . Infatti, dall’uguaglianza
. Infatti, dall’uguaglianza ![]() * 149.600.000.000.000 mm = 125 mm otteniamo:
* 149.600.000.000.000 mm = 125 mm otteniamo: ![]() = 8,3556149E-13. Ed applicando i logaritmi avremo n = 40,122319.
= 8,3556149E-13. Ed applicando i logaritmi avremo n = 40,122319.
[8] Applicando la (2b) ed imponendo per il denominatore del secondo membro la distanza minima di 125 mm:
[9] Più esattamente: K = 0,92975
[10] In questo caso il valore di X della (2c) sarebbe pari a: 6,9545E+11/0,581 = 1,19699E+12 e quindi![]() da cui K = 1.
da cui K = 1.
[11] La lente dell’obiettivo della macchina fotografica fa quello che farebbe una qualsiasi lente biconvessa e cioè creare una immagine focale rimpicciolita dell’oggetto posto all’infinito. La dimensione dell’immagine dipende poi dalle dimensioni della lente e quindi dalla sua distanza focale. Più grande è il diametro della lente maggiore sarà la sua focale e più grande anche l’immagine creata. È possibile verificare tale correlazione tra la dimensione dell’immagine e la distanza focale (e quindi la dimensione della lente) provando a mettere a fuoco, sulla medesima superficie, lo stesso oggetto, posto ad una certa distanza, usando due lenti di ingrandimento di diametro differente. La lente più grande creerà anche una immagine più grande dell’oggetto. L’obiettivo della macchina fotografica con focale 125 mm creerà quindi un’immagine del disco solare proporzionale alla sua distanza focale. Così nel calcolo appena fatto considerando la dimensione angolare del Sole, se si moltiplica l’intera distanza Terra-Sole per la tangente della dimensione angolare medesima, la dimensione ottenuta è proprio quella del diametro solare.
[12] Se ulteriori misure fotografiche lo confermassero diventa evidente che la costante 125 presente nell’equazione dipenderebbe dalla distanza focale della macchina fotografica utilizzata. Cambiando apparecchiatura cambierebbe anche il valore di questo parametro.
[3] Prendendo in considerazione il rapporto tra il valore del raggio dell’immagine lunare appena trovato (0,608) e quello relativo al Sole (0,625) cioè il valore 0,9723(2) è possibile verificare una certa coerenza di proporzionalità del valore trovato per la Luna con i valori della dimensione angolare di Luna e Sole riportati nella tabella di Fig. 2. Infatti, se calcoliamo la media dei due valori (massimo e minimo) della dimensione angolare riportati per il Sole, pari a 1921”, e moltiplichiamo tale valore per 0,9723(2) otteniamo il valore di 1867,7”. Tale valore è intermedio tra il valore minimo e quello massimo della dimensione angolare della Luna.
[14] Confronta con: https://www.astronomiamo.it/DivulgazioneAstronomica/Area/Unit%C3%A0%20di%20misura%20in%20Astronomia/Dimensione-e-massa-in-astronomia-tecniche-di-misurazione.